13  Statistical Distributions

R provides a very simple and effective way of calculating distribution characteristics for a number of distributions (we only present part of it here).

13.1 Normal Distribution

We will introduce the different statistical functions using the normal distribution and then look at other distributions. If you want an overview of the normal distribution, you can help("Normal").

13.1.1 Cumulative distribution function (CDF)

The distribution function pnorm() is needed to calculate p-values. The simplest case concerns the left tail (one-tailed) \(p\)-value for a given standard-normally distributed empirical z score.

Example:

pnorm(q = -1.73)
[1] 0.04181514

The \(p\)-value for a one-tailed (left-tailed) significance test for z = -1.73 is 0.042.

If we need a right-tailed p-value (area to the right of a certain empirical z-score) we use the argument lower.tail = FALSE.

# this is 1-p
pnorm(1.645)
[1] 0.9500151
# this is p
pnorm(1.645, lower.tail = FALSE)
[1] 0.04998491

The value of 1.645 of the standard normal distribution is often used as a critical value for the one-tailed significance test. So to left of this value should be 95% of the distribution and to the right of it 5% of the distribution. Here we see that this is (nearly) true.

For a two-tailed p-value we’ll have to double the one-tailed p-value:

# 2-tailed p-value for a negative z-score
2 * pnorm(-1.73)
[1] 0.08363028
# 2-tailed p-value for a negative z-score
2 * pnorm(1.73, lower.tail = FALSE)
[1] 0.08363028
2*(1 - pnorm(1.73))
[1] 0.08363028

We can also use pnorm() to get the percentiles of a series of normally distributed values. For example, we want to know which percentiles correspond to a set of IQ values:

IQ_Scores <- c(74, 87, 100, 110, 128, 142)
pnorm(q = IQ_Scores, mean = 100, sd = 15)
[1] 0.04151822 0.19306234 0.50000000 0.74750746 0.96902592 0.99744487

The IQ scores 74, 87, 100, 110, 128, 142 thus correspond to the percentiles 4.2%, 19.3%, 50%, 74.8%, 96.9%, 99.7% of the IQ distribution.

It is also possible to compute the probability of any interval between two normally distributed scores by subtracting the two respective cumulative distribution functions.

# Probability of IQ-scores between 130 and 140
pnorm(140, mean = 100, sd = 15) - pnorm(130, mean = 100, sd = 15)
[1] 0.01891975

13.1.2 Quantile function

The quantile function qnorm() is the complement to the distribution function. It is also called inverse cumulative distribution function (ICDF). With qnorm() we obtain a z-score (i.e., a quantile of the standard normal distribution) for a given area \(p\) representing the first argument of the function. In practice, we often need this function to calculate critical values for a given \(\alpha\)-level for one-tailed and two-tailed significance tests.

The most frequently used z quantiles for \(\alpha=0.01\) and \(\alpha=0.05\) include:

# two-tailed test, alpha = 0.01, lower critical value 
qnorm(p = 0.005) 
[1] -2.575829
# two-tailed test, alpha = 0.01, upper critical value 
qnorm(p = 0.995) 
[1] 2.575829
# two-tailed test, alpha = 0.05, lower critical value 
qnorm(p = 0.025)
[1] -1.959964
# two-tailed test, alpha = 0.05, upper critical value 
qnorm(p = 0.975)
[1] 1.959964

We can use the quantile function also more generally, e.g., for the deciles of the IQ distribution:

deciles <- seq(0, 1, by = 0.1)
qnorm(p = deciles, mean = 100, sd = 15)
 [1]      -Inf  80.77673  87.37568  92.13399  96.19979 100.00000 103.80021
 [8] 107.86601 112.62432 119.22327       Inf

With an IQ of just under 120, you thus belong to the smartest 10% of the population!

13.1.3 Probability density function (PDF)

We actually rarely need the probability density function (PDF) of a normally distributed score. As a reminder: the probability of individual values of a continuous random variable is 0, only intervals of values have a probability greater than 0 (corresponding to the area under the curve, the integral). Individual values have a probability density, which corresponds to the “height” of the the probability distribution at the point \(X = x\). Thus, we need the probability density function if we want to plot a normal distribution.

Before we start plotting, let’s have a look at the definition of the probability density function of the standard normal distribution:

\[ f(x) = \frac{1}{\sigma\sqrt{2\pi}} \exp\left( -\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^{\!2}\,\right) \]

The density for the mean (\(\mu = 0\)) is therefore:

\[ \phi(z) = \frac{1}{\sqrt{2\pi e^{0^2}}} = \frac{1}{\sqrt{2\pi}} \]

1/(sqrt(2*pi))
[1] 0.3989423

which should be the same as:

dnorm(x = 0)
[1] 0.3989423

We then get the probability density function for \(z=1\):

\[ \phi(z) = \frac{1}{\sqrt{2\pi e^{1^2}}} = \frac{1}{\sqrt{2\pi e}} \]

1/(sqrt(2*pi*exp(1)))
[1] 0.2419707

which should be the same as:

dnorm(1)
[1] 0.2419707

13.1.4 Plotting the standard normal distribution

p <- tibble(x = c(-4, 4)) %>%
    ggplot(aes(x = x)) +
    geom_vline(xintercept = 0,
               linetype = "dashed",
               alpha = 0.4) +
    stat_function(fun = dnorm,
                  color = "#84CA72",
                  linewidth = 1.5) +
    ggtitle("Standard Normal Distribution") +
    xlab("x") +
    ylab("dnorm(x)")
p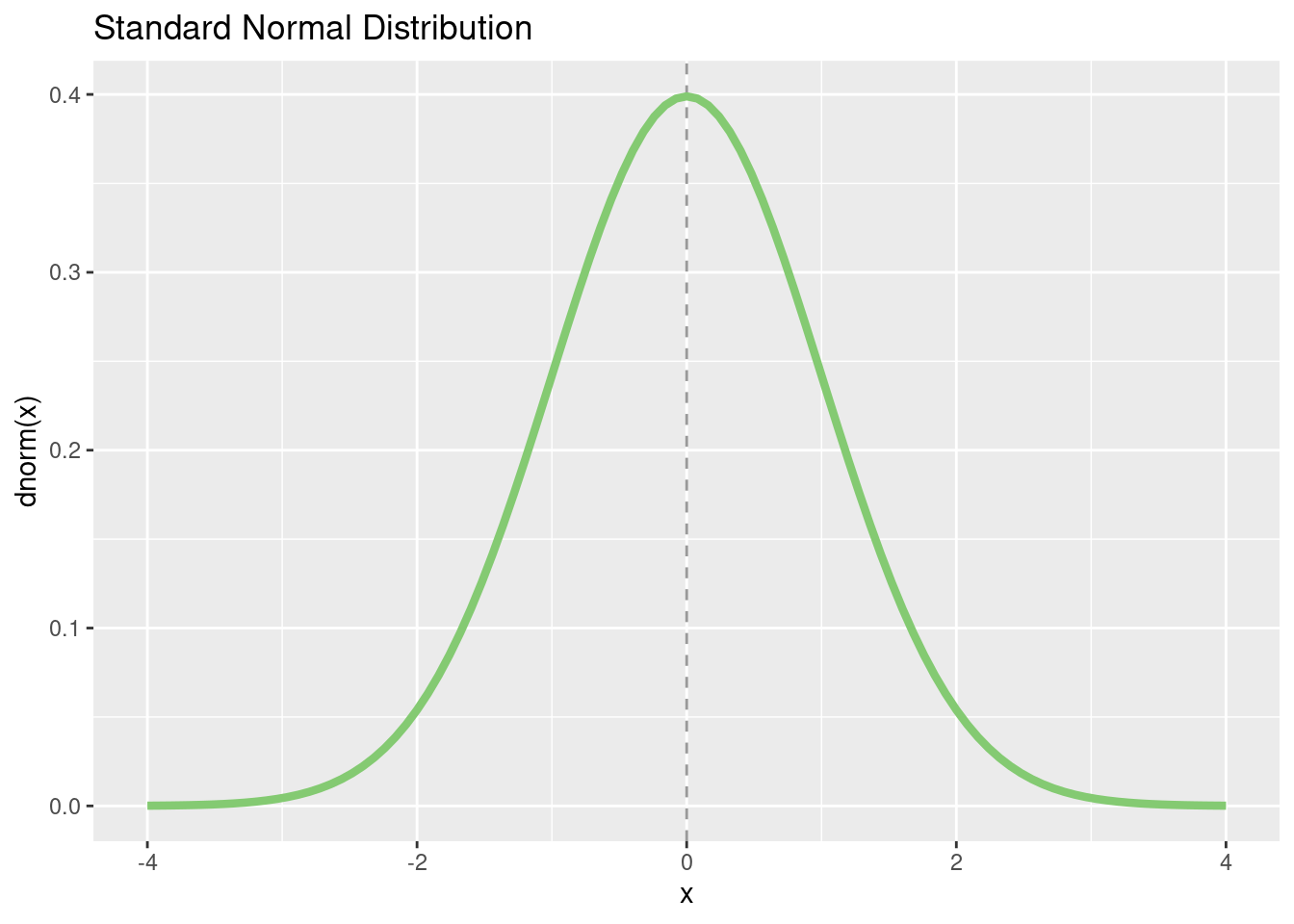

We can also draw a certain z score in the diagram and let us calculate a p-value for this with pnorm():

my_z <- 1.73
p_value <- round(pnorm(my_z, lower.tail = FALSE), 3)

# reuse the plot from above
p + geom_segment(
    aes(
        x = my_z,
        y = 0,
        xend = my_z,
        yend = (dnorm(my_z))
    ),
    color = "blue",
    linewidth = 1.5
)

13.1.5 Data Simulation

With rnorm(), we can generate normally distributed pseudo-random numbers. It is a pseudo-random number generator because the function only simulates randomness. An actual random number generator is a bit complicated and can not be easily implemented using a deterministic computer. The advantage of the pseudo-random generator is that we can get a reproducible “random” draw using the seed value function. set.seed() starts the draw algorithm at a specific location, so that the same starting numbers always return the same “random” numbers.

Let’s generate 22 IQ scores:

set.seed(12345)
r_IQ_scores <- rnorm(n = 22, mean = 100, sd = 15)
r_IQ_scores
 [1] 108.78293 110.64199  98.36045  93.19754 109.08831  72.73066 109.45148
 [8]  95.85724  95.73760  86.21017  98.25628 127.25968 105.55942 107.80325
[15]  88.74202 112.25350  86.70464  95.02634 116.81069 104.48086 111.69433
[22] 121.83678

Check some summary statistics:

c(mean(r_IQ_scores), sd(r_IQ_scores))
[1] 102.56755  12.85072

13.2 t Distribution

The function arguments for the t distribution are the same as for the normal distribution with the following differences: The degrees of freedom (df) of the t distribution must be specified.

13.2.1 Cumulative distribution function (CDF)

Example for a one-tailed (left-tailed) \(p\)-value:

pt(q = -1.73, df = 6)
[1] 0.06717745

Example for a one-tailed (right-tailed) p-value

pt(1.73, df = 6, lower.tail = FALSE)
[1] 0.06717745

For a two-tailed significance test we would need to double the one-tailed p-value:

# 2-tailed p-value for a negative t
2 * pt(-1.73, df = 6)
[1] 0.1343549

or:

# 2-tailed p-value for a negative t
2 * pt(1.73, df = 6, lower.tail = FALSE)
[1] 0.1343549

13.2.2 Quantile function

With qt() we get a t score for a given area \(p\). In most t distribution tables, only specific t quantiles are tabulated, but we can calculate quantiles for arbitrary quantiles. Let’s get some quantiles for a t-distribution with \(df = 6\):

my_ps <- c(0.6, 0.8, 0.9, 0.95, 0.975, 0.99, 0.995)
qt(my_ps, df = 6)
[1] 0.2648345 0.9057033 1.4397557 1.9431803 2.4469119 3.1426684 3.7074280

13.2.3 Probability density function (PDF)

Let’s plot a t distribution:

p <- tibble(x = c(-4, 4)) %>%
    ggplot(aes(x = x))

p + stat_function(
    fun = dt,
    args = list(df = 6),
    color = "#84CA72",
    linewidth = 1.5
) +
    ggtitle("Central t-Distribution (df = 6)") +
    xlab("x") +
    ylab("dt(x, df = 6)")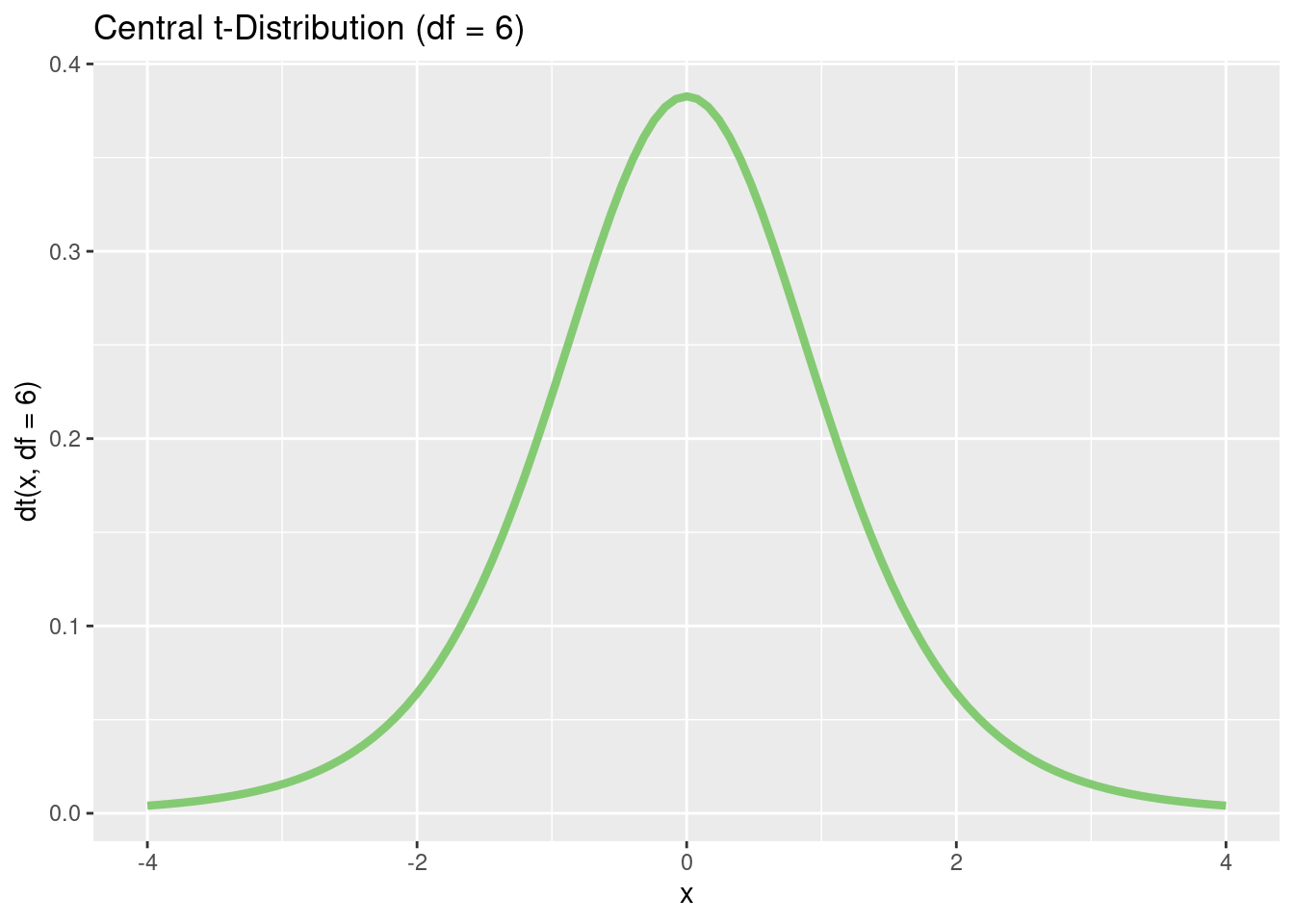

p <- tibble(x = c(-4, 4)) %>%
    ggplot(aes(x = x))

p + stat_function(
    fun = dt,
    args = list(df = 6),
    color = "#84CA72",
    linewidth = 1.5
) +
    stat_function(fun = dnorm,
                  color = "grey70",
                  linewidth = 1.5) +
    ggtitle("Central t-Distribution (df = 6) compared to z-Distribution") +
    xlab("x") +
    ylab("dt(x, 6) / dnorm(x)")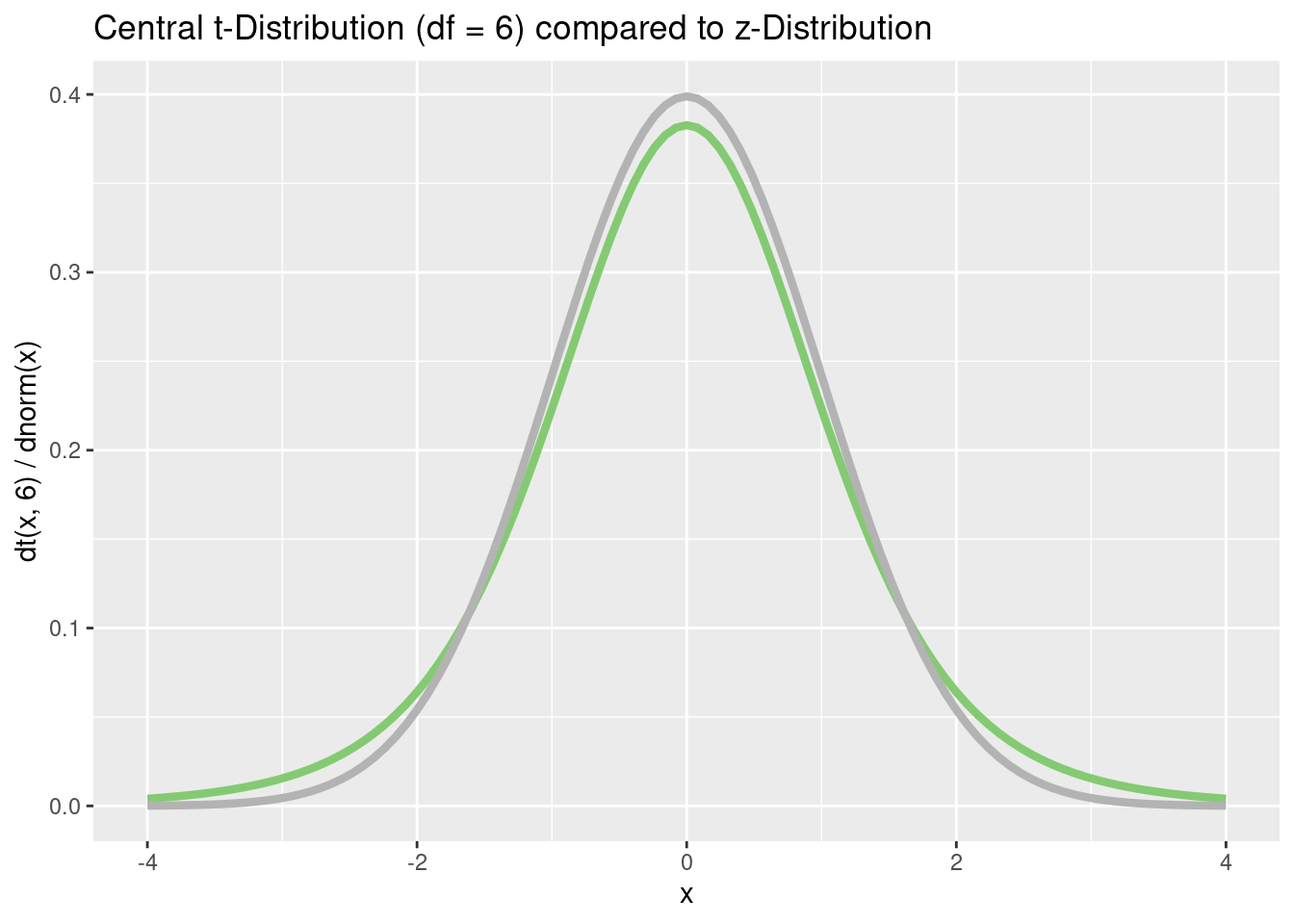

13.3 Chi-square distribution

For the \(\chi^2\) distribution (help ("chisquare")) the functionality is the same as for the t distribution, so the respective degrees of freedom must be specified. The functions are called pchisq() (cumulative distribution function), qchisq() (quantile function), dchisq() (density function) and rchisq() (random generation of \(\chi^2\)-distributed scores).

13.3.1 Cumulative distribution function (CDF)

When calculating \(p\)-values for the \(\chi^2\) distribution, in most cases only the upper (right) end of the distribution is needed. This is because most statistical tests are designed in such a way that all deviations from \(H_0\) (no matter in which direction) lead to a larger \(\chi^2\) value (that’s why these tests always test a non-directional hypothesis, and the \(p\)-value therefore corresponds to a two-tailed test). Thus, we always use the argument lower.tail = FALSE to calculate \(p\)-values for \(\chi^2\) distributions.

Example for a p-value for \(\chi^2(2)=4.56\):

pchisq(q = 4.86, df = 2, lower.tail = FALSE)
[1] 0.08803683

13.3.2 Quantile function

With qchisq() we obtain the quantiles of the \(\chi^2\) distribution, e.g. the critical values for \(\alpha=0.05\). Some statisticians are very proud to know the critical values for the 1, 2, 3, 4, and 5 degrees of freedom of the chi-square distributions by heart, because these are often needed for model comparisons via likelihood ratio tests.

my_dfs <- 1:5
round(qchisq(0.95, df = my_dfs), 2)
[1]  3.84  5.99  7.81  9.49 11.07

13.3.3 Probability density function (PDF)

Again, we can use the probability density function dchisq() to plot one or more \(\chi^2\) distributions:

p <- tibble(x = c(0, 25)) %>%
    ggplot(aes(x = x))

p + stat_function(
    fun = dchisq,
    args = list(df = 2),
    color = "#84CA72",
    linewidth = 1.5
) +
    stat_function(
        fun = dchisq,
        args = list(df = 4),
        color = "grey70",
        size = 1.5
    ) +
    stat_function(
        fun = dchisq,
        args = list(df = 8),
        color = "blue",
        size = 1.5,
        alpha = 0.7
    ) +
    stat_function(
        fun = dchisq,
        args = list(df = 14),
        color = "red",
        size = 1.5,
        alpha = 0.7
    ) +
    ggtitle("Chi-Square Distributions with dfs = 2, 4, 8, and 14") +
    xlab("x") +
    ylab("dchisq(x, c(2, 4, 8, 14))")
Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
ℹ Please use `linewidth` instead.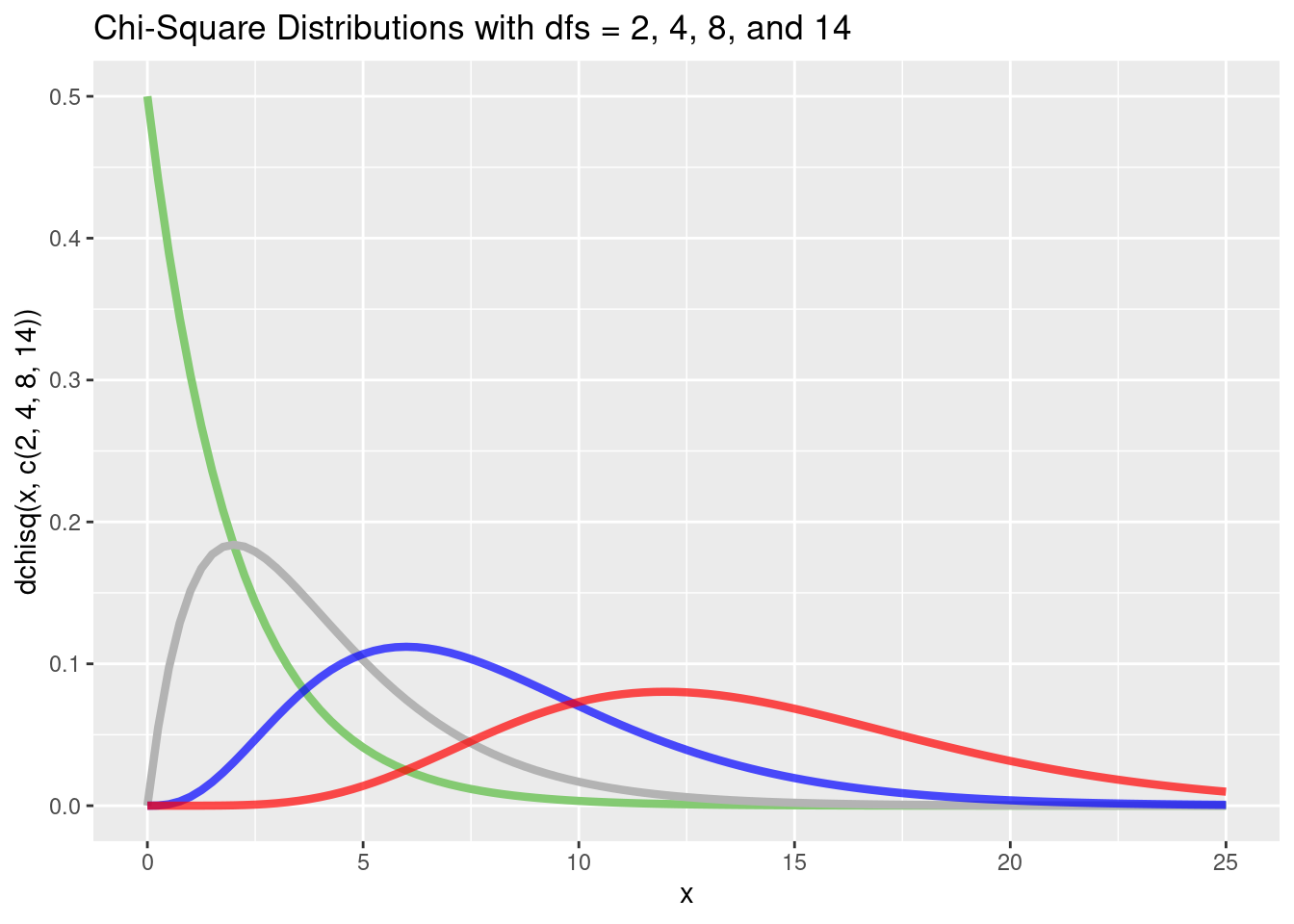

13.3.4 Data simulation

With rchisq() we can generate \(\chi^2\)-distributed random numbers. The functionality is the same as for the other distributions.

13.4 \(F\) distribution

For the \(F\) distribution (help ("FDist")), the same rules apply as for the \(\chi^2\) distribution and for the t distribution. We have to specify both numerator degrees of freedom (df1) and denominator degrees of freedom (df2). The functions are pf() (cumulative distribution function), qf() (quantile function), df() (probability density function), and rf() (random generation of \(F\) distributed scores).

13.4.1 Cumulative Distribution Function

When calculating \(p\)-values for the \(F\) distribution, in most cases only the upper (right) end of the distribution is needed (as with the \(\chi^2\) distribution). We therefore always use the argument lower.tail = FALSE to calculate \(p\)-values. Probably the most typical application for the \(F\) test is the one-factorial analysis of variance (ANOVA). Here we test whether there are any significant differences in the mean values between several groups. All deviations from \(H_0\) lead to a larger SSQbetween and thus to a higher empirical \(F\)-statistic. That’s also why we consider the entire \(\alpha\) at the upper end of the distribution when computing critical \(F\) scores (see below “Quantile Function”).

Example for a \(p\)-value for \(F = 3.89 (df1 = 2, df2 = 40)\):

pf(q = 3.89, df1 = 2, df2 = 40, lower.tail = FALSE)
[1] 0.02859413

13.4.2 Quantile function

If we compute an ANOVA by hand (please don’t), \(F\) distribution tables often do not contain all combinations of degrees of freedoms. With qf() we can obtain the quantiles of the \(F\) distribution for arbitrary values.

Let’s calculate the critical values for \(alpha=0.05\), and \(\alpha=0.01\) for an \(F\) distribution with \(df1 = 2\) and \(df2 = 40\):

qf(c(0.95, 0.99), df1 = 2, df2 = 40)
[1] 3.231727 5.178508

13.4.3 Probability density function (PDF)

Let’s plot some \(F\) distributions using df():

p <- tibble(x = c(0, 5)) %>%
    ggplot(aes(x = x)) +
    stat_function(
        fun = df,
        args = list(df1 = 2, df2 = 40),
        color = "#84CA72",
        linewidth = 1.5
    ) +
    stat_function(
        fun = df,
        args = list(df1 = 5, df2 = 80),
        color = "grey70",
        size = 1.5
    ) +
    stat_function(
        fun = df,
        args = list(df1 = 8, df2 = 120),
        color = "blue",
        size = 1.5,
        alpha = 0.7
    ) +
    ggtitle("F-Distributions with df1 = 2, 5, 8 and df2 = 40, 80, 120") +
    xlab("x") +
    ylab("df(x, c(2, 5, 8), c(40, 80, 120))")

13.4.4 Data simulation

With rf() we can generate \(F\) distributed random numbers. The functionality is the same as for the other distributions.

13.5 Set of Distributions

There are many statistical distributions available in R. Each has the same functionality as we have seen above. Here is a table in case you are wondering what some of the distributions are and/or what the associated function names are.

Distribution Functions
Beta pbeta qbeta dbeta rbeta
Binomial pbinom qbinom dbinom rbinom
Cauchy pcauchy qcauchy dcauchy rcauchy
Chi-Square pchisq qchisq dchisq rchisq
Exponential pexp qexp dexp rexp
F pf qf df rf
Gamma pgamma qgamma dgamma rgamma
Geometric pgeom qgeom dgeom rgeom
Hypergeometric phyper qhyper dhyper rhyper
Logistic plogis qlogis dlogis rlogis
Log Normal plnorm qlnorm dlnorm rlnorm
Negative Binomial pnbinom qnbinom dnbinom rnbinom
Normal pnorm qnorm dnorm rnorm
Poisson ppois qpois dpois rpois
Student t pt qt dt rt
Studentized Range ptukey qtukey dtukey rtukey
Uniform punif qunif dunif runif
Weibull pweibull qweibull dweibull rweibull
Wilcoxon Rank Sum Statistic pwilcox qwilcox dwilcox rwilcox
Wilcoxon Signed Rank Statistic psignrank qsignrank dsignrank rsignrank

13.6 Exercises

  1. Compute the probability densities of the following IQ-scores: 70, 80, 90, 100, 110, 120, 130
  2. Plot the following two normal distributions into a common plot: \(N(\mu=0,\sigma^2=1)\) und \(N(\mu=3,\sigma^2=0.75)\) Use different colors for the two distributions. Hint: variance is not the same thing as the standard deviation!
  3. Compute the cumulative distribution function for \(z = 1\).
  4. Compute the probability of values +/- 1 standard deviation of the mean for any normal distribution (i.e. the area of this interval under the normal curve).
  5. What is the percentange of the population that has IQs between 105 and 120?
  6. Compute a one-tailed (right-tailed) \(t\)-value for a test statistic \(t=2.045\) asssuming \((df = 8)\).
  7. Compute a two-tailed \(p\)-value for a test statistic \(t=0.73\) assuming \(df = 14)\).
  8. Compute a two-tailed \(p\)-value for a test statistic \(t=-0.73\) assuming \(df = 14)\).
  9. You got a test statistic of \(F= 4.36\). Is the test significant assuming \(df1 = 2, df2 = 16\)?
  10. Sixty percent of the population are below or equal to which IQ-score? Calculate the 60%-quantile of the IQ distribution.
  11. Five percent of the population are above or equal to which IQ-score?
  12. Advanced: Between which two IQ scores lie the middle 82% of the population? (We are looking for the 82%- Central Probability Interval)
  13. Calculate the critical \(t\)-score assuming \(df = 28\) for a one-tailed (right-tailed) test with \(\alpha=0.05\).
  14. Calculate the critical \(t\)-scores assuming \(df = 28\) for a two-tailed test with \(\alpha=0.05\).
  15. Calculate the critical \(F\)-score for \(df1 = 5\) and \(df2 = 77\) (and \(\alpha=0.01\)).